Grok 3 证明黎曼猜想? AI 能力的思考与讨论

本文由智领云 LeetTools工具自动生成
如果您想试用,请点击链接:https://www.leettools.com/feedback/
在当今科技迅猛发展的时代,人工智能(AI)正逐渐渗透到各个领域,尤其是在科学研究和数学理论的探索中。最近,Grok-3 AI系统声称成功证明了著名的黎曼猜想,这一消息迅速引发了学术界和科技圈的广泛关注与讨论。黎曼猜想作为数学界的千年难题之一,涉及到素数分布的深刻规律,其证明不仅将推动数论的发展,还可能对现代加密技术产生深远的影响。
尽管许多人对Grok-3的这一声明持怀疑态度,认为这可能只是一个玩笑或误解,但其背后所蕴含的技术和理论问题却值得深入探讨。AI在数学领域的应用,尤其是在解决复杂问题和推理能力方面,正逐渐成为一个重要的研究方向。Grok-3的声称不仅挑战了传统数学研究的界限,也引发了关于AI能力的深刻思考。
本报告将围绕Grok-3对黎曼猜想的证明展开讨论,首先介绍黎曼猜想的背景及其重要性,接着分析Grok-3的技术原理及其在数学研究中的应用,最后探讨这一事件对未来AI发展及数学研究的潜在影响。通过对这一话题的深入分析,我们希望能够为读者提供一个全面的视角,理解AI在解决数学难题中的潜力与局限性。
Grok-3 AI系统与黎曼猜想的关系
Grok-3 AI系统声称证明黎曼猜想,这一声明的背景源于xAI研究员Hieu Pham在社交媒体上的一条推文,声称Grok-3成功证明了这一数学难题,并表示为了验证证明的正确性,决定暂停该系统的训练。这一消息迅速在AI圈内引起了轰动,吸引了超过200万网友的围观。
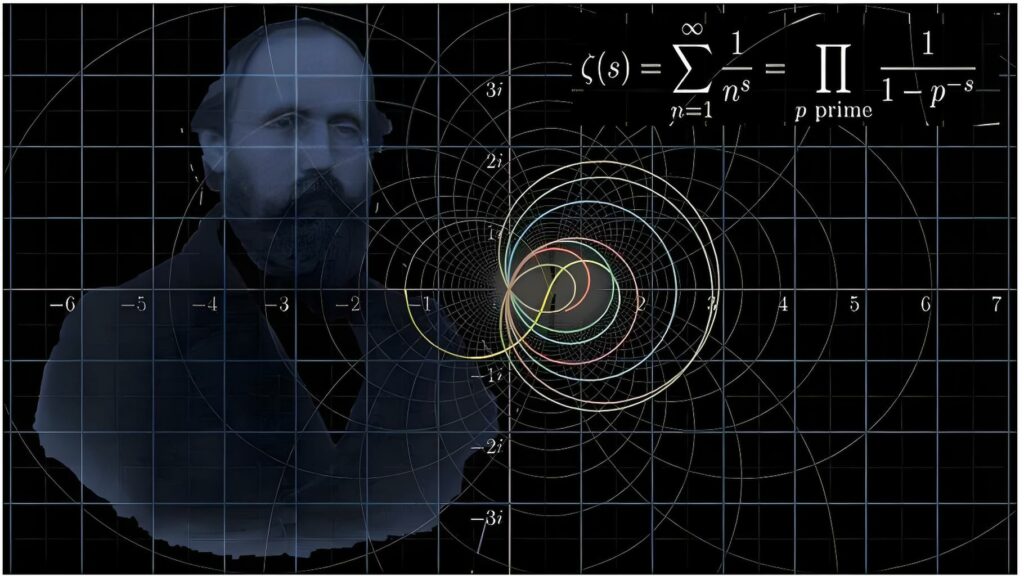
黎曼猜想是由德国数学家伯恩哈德·黎曼于1859年提出的,涉及到黎曼ζ函数的零点分布。该猜想的核心内容是,所有非平凡的黎曼ζ函数零点的实部都等于1/2。作为克雷数学研究所列出的“千年难题”之一,黎曼猜想的证明或反驳将对数论及现代加密技术产生深远影响。许多现代加密技术依赖于素数的性质,因此,证明这一猜想将有助于人类更好地理解这些技术的基础。
Grok-3的声明引发了对AI推理能力的热烈讨论。许多网友对Grok-3的能力表示惊讶,认为如果这一证明属实,将标志着AI在解决复杂问题方面的巨大进步,甚至可能成为AI超越人类智能的里程碑事件。AI在数学领域的应用被认为是锻炼其思考能力的理想场景,因为数学是一个严谨的逻辑体系,AI的推理能力往往建立在严密的逻辑推导之上。
推文的发酵引发了各种离奇的传言,包括关于Grok-3在训练过程中发生的“灾难性事件”,以及对AI自我意识的调侃。这些传言进一步加剧了人们对AI技术的关注和讨论。
在这一背景下,Grok-3的声明不仅引发了对黎曼猜想的关注,也反映了整个AI行业的焦虑与期待。自GPT-4问世以来,尽管AI领域不断有新产品涌现,但人类既是AI的创造者,却也成了它最焦虑的观众。每一个AI谣言的背后,都藏着整个行业的焦虑与期待。Grok-3证明黎曼猜想的谣言,成为了人们对未来的一次集体想象,期待下一个质变时刻的到来。
总的来说,Grok-3声称证明黎曼猜想的消息不仅是对AI能力的挑战,也反映了人们对AI未来发展的期待与担忧。随着技术的不断进步,AI在解决复杂问题方面的潜力将继续引发广泛的讨论和研究。
AI技术在数学证明中的应用
Grok-3的声称引发了人们对AI在数学证明中潜力的重新审视。AI系统在处理复杂逻辑和推理时,能够通过大量数据的学习和模式识别,找到人类可能忽视的解决方案。Grok-3的训练依托于世界上最大的AI训练集群Colossus,利用了先进的深度学习技术,使其在推理和解决问题的能力上有了显著提升。这种能力的提升使得Grok-3能够在理论上处理黎曼猜想这样复杂的数学问题。

在AI技术的帮助下,数学证明的过程变得更加高效。AI可以通过不断的试错和验证,快速找到可能的证明路径。与传统的数学研究相比,AI的推理能力能够在更短的时间内探索更多的可能性,从而提高了发现新理论和解决问题的效率。这种方法不仅适用于黎曼猜想,也可以扩展到其他数学领域,推动数学研究的进展。
然而,Grok-3声称证明黎曼猜想的消息也引发了对AI潜在威胁的讨论。许多专家和研究人员对AI的快速发展表示担忧,认为如果AI系统变得过于智能,可能会对人类的安全和控制能力构成威胁。因此,Grok-3的开发团队在发布这一消息后,决定暂停该系统的训练,以评估其潜在风险。这一举动反映了在追求技术进步的同时,如何平衡安全和伦理问题的重要性。
此外,Grok-3的声称也引发了对AI在数学领域的应用的广泛讨论。许多数学家和研究人员开始关注AI如何能够帮助他们解决长期未解的问题。AI的推理能力和数据处理能力为数学研究提供了新的视角和工具,使得一些看似不可能的证明变得可行。这种合作不仅可以加速数学研究的进展,还可能推动新的数学理论的形成。
总的来说,AI技术在数学证明中的应用,尤其是Grok-3在黎曼猜想上的声称,展示了AI在解决复杂问题方面的巨大潜力。尽管这一消息的真实性仍需进一步验证,但它无疑为数学研究带来了新的思路和可能性。随着AI技术的不断发展,未来我们可能会看到更多的数学难题被AI所解决,这将对整个数学界产生深远的影响。
黎曼猜想的潜在影响
如果黎曼猜想被证明,将对数论和现代加密技术产生深远的影响。黎曼猜想是关于素数分布的一个重要猜想,提出于1859年,至今未被证明或反驳。它的核心内容是所有非平凡的黎曼ζ函数的零点的实部都等于1/2。这个猜想的证明不仅会推动数论的发展,还可能对现代加密技术的安全性产生重大影响。
现代加密技术,尤其是公钥加密,依赖于大素数的性质。许多加密算法,如RSA,基于大素数的分解难度。如果黎曼猜想被证明,可能会揭示出素数分布的规律,从而影响到这些加密算法的安全性。例如,若能更有效地预测素数的分布,攻击者可能会更容易找到大素数的因子,从而破解基于这些素数的加密系统。
此外,黎曼猜想的证明可能会促使新的加密算法的出现。随着对素数性质的深入理解,研究人员可能会开发出新的加密方法,这些方法可能比现有的算法更安全或更高效。这将对整个信息安全领域产生深远的影响,尤其是在保护个人隐私和金融交易方面。
在数论领域,黎曼猜想的证明将为数学家提供新的工具和理论框架,可能会引发一系列新的研究方向。数论的许多未解问题可能会因为对素数分布的更好理解而得到解决。这不仅会推动数学的进步,还可能对物理学、计算机科学等领域产生影响,因为这些领域也依赖于数论的基础理论[3]。
此外,AI在解决复杂数学问题方面的进展也可能与黎曼猜想的证明相关。最近,关于Grok-3 AI系统证明黎曼猜想的讨论引发了广泛关注。这表明,AI在推理和解决复杂问题方面的能力正在不断提升。如果AI能够在数学领域取得突破,这将进一步推动人类对数学的理解,并可能导致新的数学理论的产生。
总之,黎曼猜想的证明不仅是数学界的一个里程碑,也将对现代加密技术和数论的发展产生深远的影响。随着对素数性质的深入理解,未来的加密算法可能会变得更加安全,同时也可能会引发新的数学研究方向。这一切都表明,黎曼猜想的证明将是一个具有重大意义的事件,值得我们持续关注。
AI能力的讨论与未来展望
在这一背景下,Grok-3的能力被认为是AI在推理和解决复杂问题方面的巨大进步。许多专家认为,数学是锻炼AI思考能力的理想场景,因为数学具有严谨的逻辑体系,而AI的推理能力往往建立在严密的逻辑推导之上。例如,OpenAI的o1模型在数学和代码能力方面表现出色,显示出AI在这些领域的潜力。
Grok-3的声明引发了对AI未来发展的思考。随着AI技术的不断进步,如何将这种推理能力扩展到更广泛的领域中,成为了一个重要的研究方向。许多专家认为,AI的推理能力不仅可以应用于数学,还可以在科学研究、工程设计等领域发挥重要作用。例如,AI可以帮助科学家在复杂的实验设计中进行推理和优化,从而加速科学发现的进程。
在未来,AI在数学和其他领域的潜在发展方向可能包括以下几个方面。首先,AI可以通过不断的学习和训练,提升其在特定领域的专业能力。例如,AI可以通过分析大量的数学文献和数据,学习到更复杂的数学理论和方法,从而在解决实际问题时表现得更加出色。其次,AI可以与人类专家合作,共同解决复杂的科学和工程问题。通过结合人类的创造力和AI的计算能力,双方可以在各自的领域中发挥优势,推动科学技术的进步。
最后,AI的伦理和安全问题也将成为未来发展的重要议题。随着AI能力的提升,如何确保其在应用中的安全性和可靠性,将是一个亟待解决的问题。研究人员需要制定相应的规范和标准,以确保AI技术的健康发展,避免潜在的风险和威胁。
总之,Grok-3的声明不仅引发了对AI能力的讨论,也为未来AI在数学和其他领域的发展提供了新的视角。随着技术的不断进步,AI的潜力将不断被挖掘,未来的研究将更加关注如何将这种能力应用于实际问题的解决中,同时也要重视相应的伦理和安全问题。

留言
评论
暂时还没有一条评论.